Ympyrät tasossa

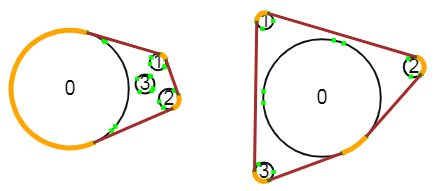
Kysymys

Olkoon tasossa $n$ toisiaan leikkaamatonta $1$ -säteistä ympyrää. (Ympyrällä tarkoitetaan sen kaarta.) Mikä on todennäköisyys, että kun valitaan näiltä piste satunnaisesti, tästä pisteestä ei näy muita ympyröitä?

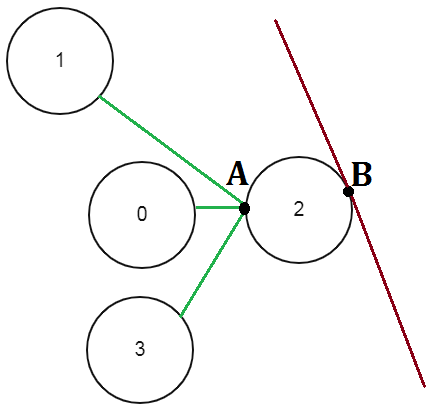
Ympyrän 2 pisteestä $A$ näkyy kaikki muut ympyrät. Pisteestä $B$ taas ei näy mikään toinen ympyrä, sillä ne ovat kaikki $B$ :hen piirretyn tangenttisuoran ”väärällä” puolella.

Kokeile:

https://Invisible-Circles–minkkilaukku2.repl.co

Ratkaisu

Vastaus on $\begin{aligned} \frac{1}{n} \end{aligned}$ .

Ja tämä siis aivan riippumatta ympyröiden sijainneista (paitsi eivät saa leikata toisiaan, kuten sovittiin).

Todistuksen runko

Ympyröiden konveksiverho $C$ . Kaariosuudet keltaisella ja janaosuudet ruskealla. Vihreät pisteet ympyröillä ovat niiden välisten tangenttijanojen päätepisteitä, ”kaikkein uloimmaiset” tangenttijanat ovat mukana $C$ :ssä.

Olkoon $C_0$ ympyröiden yhdisteen konveksiverho.
Joukon $C_0$ reuna $C$ on janoista ja ympyränkaarista koostuva derivoituva Jordanin käyrä.
Ympyrän piste $P$ kuuluu $C$ :hen täsmälleen silloin, kun se on sellainen piste, josta ei näy mikään muu ympyrä. (Pois lukien äärellisen monta pistettä, jotka ovat $C$ :n janojen päätepisteitä: janat ovat ympyröiden välisiä tangentteja, joten niiden päätepisteet leikkaavat kahta ympyrää, joten niistä on näköyhteys. Näiden joukko on kuitenkin äärellisenä nollamittainen eikä vaikuta todennäköisyyteen.)
Käyrän $C$ kokonaiskaarevuus on $\begin{aligned} \int_{a}^b \kappa (s) ds = 2\pi \end{aligned}$ , sillä kierrosluku on $1$ .
Toisaalta $\begin{aligned} \int_{a}^b \kappa (s) ds \end{aligned}$ on käyrällä $C$ olevien ympyränkaarien yhteenlaskettu mitta, sillä janaosuudella kaarevuus $\kappa = 0$ ja kaariosuudella $\kappa = \frac{1}{1} = 1$ , sillä jokaisen ympyrän säde on $1$ (ks. kaarevuudesta Wikipediassa).
Siis suotuisan osan mitta on $2\pi$ . Kaikkien ympyröiden mitta on $2\pi n$ , joten väite seuraa.

Huomioita

Yleistyy kolmiulotteiseksi: pallot 3D-avaruudessa. Gauss-Bonnet:n lause.
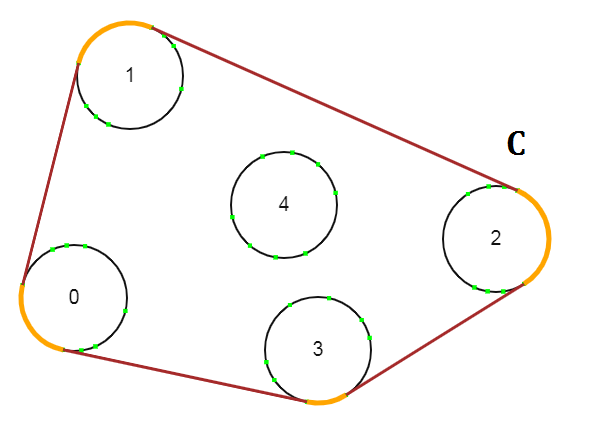
Jos ympyröiden säteet ovat eri suuruisia, ympyröiden paikat vaikuttavat tulokseen. Tämä johtuu siitä, yo. integraalissa kaarevuus ei ole joka ympyrällä vakio vaan tulos riippuu siitä millaisia ympyröitä ulkokaaressa on mukana minkäkin verran. Ks. esimerkkikuva alla.

Ympyrät tasossa

Kysymys

Kokeile:

Ratkaisu

Todistuksen runko

Huomioita

Julkaissut membolic

Jätä kommentti Peruuta vastaus

Kysymys

Kokeile:

Ratkaisu

Todistuksen runko

Huomioita

Jaa:

Aiheeseen liittyy

Julkaissut membolic

Jätä kommentti Peruuta vastaus