Rauhalliset ratsut

Kysymys:

Kuinka monella tavalla voidaan $n\times n$ -laudalle asettaa 4 ratsua, siten että mikään ei uhkaa toista? Kaikki ratsut ovat identtisiä ja vihollisia keskenään.

Ratkaisu:

Merkitään $V = [1..n]^2$ eli kaikkien laudan ruutujen joukko. Kaikki mahdolliset neljän ratsun asettelut ovat nyt joukko

$\begin{aligned} S=\{(v_1, v_2, v_3, v_4) \in V^4 \text{ } | \text{ } v_i \neq v_j \text{, kun } i \neq j \} \end{aligned}.$

Määritellään kaarijoukko $E$ kuvastamaan sitä mihin ruutuun kustakin ruudusta ratsu voi liikkua, eli mitä kaikkia ruutuja se uhkaa. (Huom. ratsuissa on se mukava juttu, että ne eivät välitä laudan muista nappuloista vaan voivat hypätä näiden yli.) Näin saadaan $n\times n$ –ratsun graaf i.

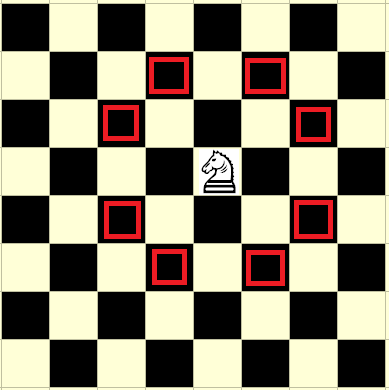
Ratsun liikkumismahdollisuudet ovat 1 ruutu vaakasuunnassa ja 2 ruutua pystysuunnassa, tai kääntäen.

Tehdään tässä välissä sellainen huomio, että ratsun graafilla ei ole kolmioita: mitkään kolme eri ratsua (kun ovat laudalla eri ruuduissa) eivät voi uhata kaikki toisiaan. Tämä johtuu siitä, että ratsu vaihtaa aina liikkuessaan väriä: se liikkuu yhteensä kolme askelta mustalta valkealle / valkealta mustalle. Kolmesta ratsusta vähintään kaksi on samalla värillä, joten ne eivät voi uhata toisiaan. Ratsun graafi on juuri tämän värin vaihtamisen takia kaksijakoinen (valkeat ja mustat ruudut).

Määritellään joukot $\begin{aligned} A_{ij} = \{ (v_1, v_2, v_3, v_4) \in S \text{ } | \text{ } v_i \text{ ja } v_j \text{ uhkaavat toisiaan} \} \end{aligned}$ . Tarvitsemme joukkoja $A_{12}, A_{13}, A_{14}, A_{23}, A_{24}$ ja $A_{34}$ , sillä kysytty lukumäärä on joukon $S \setminus \cup_{ij\in I} A_{ij}$ koko. Indeksijoukko $I := \{ 12, 13, 14, 23, 24, 34\}$ (huom. merkinnät 12,… eivät aiheuta sekaannusta, sillä luvut pysyvät alle kymmenen). Voimme laskea inkluusio-eksluusiolla:

$\begin{aligned} \left |S\setminus \bigcup_{ij\in I} A_{ij} \right | = \sum_{J\subset I} (-1)^{|J|} \left|\bigcap_{ij \in J} A_{ij} \right| \end{aligned},$

missä leikkaus tyhjän joukon yli tarkoittaa koko joukkoa $S$ . Tehtävän ratkaisemiseksi meidän on siis laskettava kaikkien erilaisten leikkausten $\cap_{J} A_{ij}$ koot. Monet näistä ovat symmetrian nojalla samoja ja osa graafin kolmio-vapauden takia mahdottomia. Ne jakautuvat seuraaviin luokkiin:

Erilaiset leikkaustyypit. Solmut ovat indeksejä $i$ ja $j$ , kaari näiden välillä tarkoittaa että $A_{ij}$ on leikkauksessa mukana. Viereen merkitty kuinka monta kutakin leikkaustyyppiä on (symmetria, kuvassa on aina vain esimerkki numerointi solmuille). Taso, eli kuinka monta joukkoa leikkauksessa on, merkitty alle. Huomaa että tason $t$ kaikkinainen lukumäärä on ${{6}\choose{t}}$ : leikkaukseen valitaan $t$ joukkoa kaikista kuudesta. Kolmion sisältävät ovat mahdottomia eli niitä vastaavat leikkaukset ovat tyhjiä.

Merkitään

$\begin{aligned} a_1 =& |A_{12}| = |A_{13}| = \dots = |A_{34}| \\ a_{21} =& |A_{12} \cap A_{13}| = |A_{13} \cap A_{14}| = \dots = |A_{14} \cap A_{24}| \\ a_{22} =& |A_{12} \cap A_{34}| = |A_{13} \cap A_{24}| = |A_{14} \cap A_{23}| \\ a_{31} =& |A_{12} \cap A_{13} \cap A_{14} | = \dots = |A_{14} \cap A_{24} \cap A_{34} | \\ a_{32} =& |A_{12} \cap A_{23} \cap A_{34} | = \dots \\ a_{4} =& |A_{12} \cap A_{23} \cap A_{34} \cap A_{14} | = \dots \end{aligned}$

Siis $a_1 =$ kaaret (ja kaksi muuta saa olla mitä vain muita solmuja), $a_{21} =$ 2-ketjut (ja viimeinen saa olla mikä vain muu solmu), $a_{22} =$ erilliset kaaret, $a_{31} =$ kaikki yhden naapureita, $a_{32} =$ 4-ketjut ja $a_{4} =$ 4-syklit.

Tällöin kysytty lukumäärä on

$\begin{aligned} \frac{1}{24}(n^2(n^2-1)(n^2-2)(n^2-3) - 4a_1 + 12a_{21} + 3a_{22} - 4a_{31} - 12a_{32} + 3a_{4}) \end{aligned}$

Tässä on sijoitettu $|S| = n^2(n^2-1)(n^2-2)(n^2-3)$ ja jakaja $24=4!$ tulee siitä, että ratsujen järjestyksellä ei ole kysymyksessä väliä, mutta me laskimme järjestettyjä nelikoita.

Tällaisten konfiguraatioiden laskemista graafilla käsittelimme viime kertojen postauksissa: Erillisten kaariparien laskeminen ja Graafin naapuruus-polynomeja. Meillä oli apuna graafin naapuruus-polynomit. Koitetaan siis selvittää ne ratsun $n\times n$ -graafille. Laskeminen eri arvoille paljastaa melko nopeasti säännönmukaisuuden, jonka voi sitten kuvaa katsomalla perustella. Polynomi $p_1$ on helppo: nurkilla on jokaisella 2 naapuria, näiden viereisillä ( $8$ :lla) reunaruuduilla 3, muilla ( $4(n-4)$ ):lla reunaruuduilla 4. Toisella rinkulalla käy näin: nurkat: 4, muut reunat ( $4(n-4)$ ): 6. Sitä sisemmillä on kaikilla täydet 8 naapuria. Saamme siis, kun $n\geq 5$

$\begin{aligned} p_1(x) = 4x^2 + 8x^3 + 4(n-3)x^4 + 4(n-4)x^6 + (n-4)^2x^8 \end{aligned}$

Pienemmille $n$ :n arvoille tämä ei toimi, mutta niille koko ongelma voidaan laskea brute-forcena.

Sitten polynomi $p_2$ . Tämä vaatii hieman enemmän pähkäilyä, mutta tapaus $8 \times 8$ oli meillä jo edellisessä postauksessa esimerkkinä. Itse asiassa tuo tapaus on juuri viimeinen, jossa yleinen kaava ei tule vielä käytäntöön. Arvoille $n\geq 9$ pätee

$p_2(y_2, y_3, y_4, y_6, y_8) =\\ 4y_6^2 \text{ } + \text{ } 8y_4y_6y_8 \text{ } + \text{ } 8y_3y_6^2y_8 \text{ } + \text{ } 8y_4y_6y_8^2 \text{ } + \text{ } 4(n-8)y_6^2y_8^2 \text{ } + \text{ } 4y_4^2y_8^2 \text{ } + \text{ } 8y_2y_4^2y_6y_8^2 \text{ } + \text{ } 8y_3y_4y_6y_8^3 \text{ } + \text{ } 4(n-8)y_4^2y_8^4 \text{ } + \text{ } 4y_3^2y_4^2y_6^2y_8^2 \text{ } + \text{ } 8y_4^3y_6^2y_8^3 \text{ } + \text{ } 4(n-8)y_4^2y_6^2y_8^4 \text{ } + \text{ } 4y_6^4y_8^4 \text{ } + \text{ } 4(n-8)y_6^2y_8^6 \text{ } + \text{ } (n-8)^2y_8^8$

Lisäksi tarvitsimme vielä polynomin $p_E$ . Se saadaan, mikäli $n \geq 7$ , kaavalla

$\begin{aligned} p_E(x) = 8 x^6 + 16 x^7 + 8 x^8 + 8(n-5)x^9 + 8x^{10} + 8(n-3)x^{11} + (16(n-6)+8)x^{13} + 4(n-5)(n-6)x^{15} \end{aligned}$

Ainoa tapaus, jota emme $a$ ’itten laskemisesta vielä käsitelleet aimmissa postauksissa on 4-syklit eli $a_4$ . Mutta näiden lukumäärälle löytyy kaava mathworldista: Jos $n\geq 4$ , niin $a_4 = 16(n^2-18n+26)$ , muuten $0$ . (Meidän täytyy kertoa mathworldin kaava $8$ :lla, sillä tutkimme järjestettyjä nelikoita.)

Huomataan, että, kun $n \geq 9$ , laskenta-algoritmit tuottavat $n$ :stä riippuvan, astetta $8$ olevan polynomin, joten sen kertoimet voidaan selvittää laskemalla interpolaatio-polynomi tarpeeksi monelle pisteelle. Saadaan

$\begin{aligned} \frac{1}{24}(n^8 - 54n^6 + 144n^5 + 1019n^4 - 5232n^3 - 2022n^2+51120n - 77184) \end{aligned}$

Huomataan, että tämä kaava toimii itse asiassa, kun $n \geq 6$ . Pienemmät arvot $1 \leq n \leq 5$ eivät noudata tätä kaavaa, mutta niille voidaan keksiä kaava

$\begin{aligned} \frac{1}{6} (723 n^4 - 6869 n^3 + 23187 n^2 - 32317 n + 15276) \end{aligned}.$

ja näin on ratkaisu saatu kahdessa palassa määrättyä.

Huomoita

Yleinen ongelma, josta tämä on esimerkki on graafin riippumattomien joukkojen numerointi.
Tämä kyseinen jono löytyy OEIS:sta. Jonon $n$ :s termi on ratsun $n\times n$ -graafin riippumattomuus polynomin neljännen asteen kerroin.

Tehtäviä

Ratkaise vastaava tehtävä, kun laudalle asetetaan 2 valkeaa ja 2 mustaa ratsua. Nyt sallittuja tilanteita ovat ne, joissa eriväriset eivät uhkaa toisiaan. (Vinkki: valitse tietyt joukot $A_{ij}$ .)
Yleistyksiä: $m\times n$ -laudalle, $k$ :lle ratsulle, $(k_1, k_2,\dots)$ eri väriselle ratsulle. Myös eri nappuloille (huom. rajoituksen että nappi ei voi mennä toisen yli voi unohtaa. Uhkaamattomassa tilanteessa sillä ei ole väliä, koska muiden nappuloiden liikkeet ovat lineaariset ja ne uhkaavat jo edessä olevaa nappulaa, jos joutuisivat kulkemaan sen läpi uhatakseen toista).
Perustele 4-syklien kaava.

Rauhalliset ratsut

Kysymys:

Ratkaisu:

Huomoita

Tehtäviä

Julkaissut membolic

Jätä kommentti Peruuta vastaus

Kysymys:

Ratkaisu:

Huomoita

Tehtäviä

Jaa:

Aiheeseen liittyy

Julkaissut membolic

Jätä kommentti Peruuta vastaus